Time-Varying ALIP Model and Robust Foot-Placement Control for Underactuated Bipedal Robotic Walking on a Swaying Rigid Surface
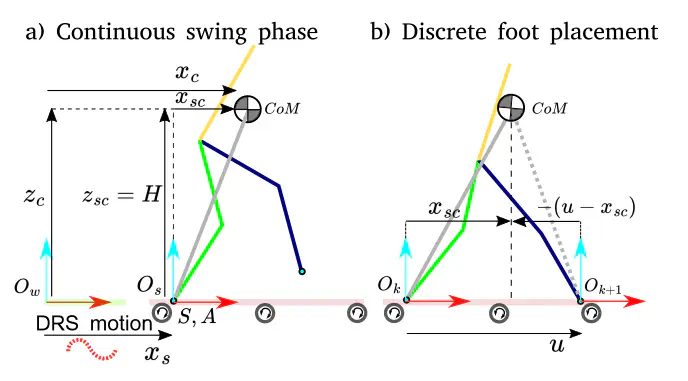 Illustration of the proposed hybrid AIP model a) during a continuous swing phase and b) at a discrete foot-landing event.
Illustration of the proposed hybrid AIP model a) during a continuous swing phase and b) at a discrete foot-landing event.Abstract
Controller design for bipedal walking on dynamic rigid surfaces (DRSes), which are rigid surfaces moving in the inertial frame (e.g., ships and airplanes), remains largely underexplored. This paper introduces a hierarchical control approach that achieves stable underactuated bipedal walking on a horizontally oscillating DRS. The highest layer of our approach is a real-time motion planner that generates desired global behaviors (i.e., center of mass trajectories and footstep locations) by stabilizing a reduced-order robot model. One key novelty of this layer is the derivation of the reduced-order model by analytically extending the angular momentum based linear inverted pendulum (ALIP) model from stationary to horizontally moving surfaces. The other novelty is the development of a discrete-time foot-placement controller that exponentially stabilizes the hybrid, linear, time-varying ALIP. The middle layer translates the desired global behaviors into the robot’s full-body reference trajectories for all directly actuated degrees of freedom, while the lowest layer exponentially tracks those reference trajectories based on the full-order, hybrid, nonlinear robot model. Simulations confirm that the proposed framework ensures stable walking of a planar underactuated biped under different swaying DRS motions and gait types.