Embedding of slip dynamics on underactuated bipedal robots through multi-objective quadratic program based control

Abstract

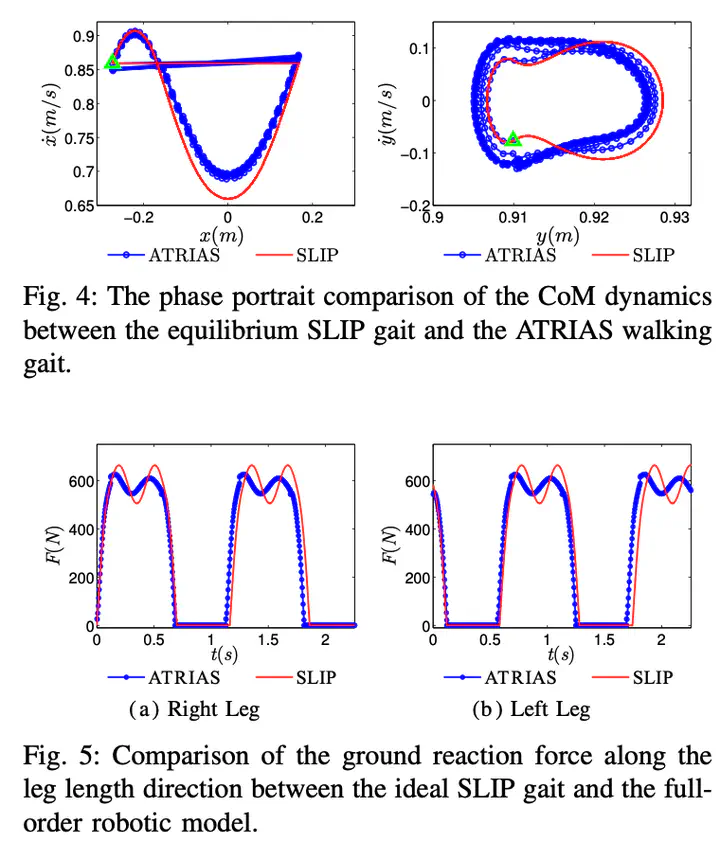
This paper presents a method for achieving stable periodic walking, consisting of phases of single and double support, on underactuated walking robots by embedding Spring Loaded Inverted Pendulum (SLIP) dynamics. Beginning with a SLIP model, the dynamics are stabilized to a constant energy level and periodic walking gaits are found; an equality constraint on torque can be used to shape the dynamics of the full-order robot to obey the corresponding SLIP dynamics. To transition these gaits to full-order robots, the essential elements of SLIP walking gaits, i.e., the swing leg touchdown angle, are utilized to synthesis control Lyapunov functions that result in inequality constraints in torque. Finally, the desired force interactions with the environment as dictated by SLIP dynamics are utilized to obtain inequality constraints in the reaction forces. Combining these equality and inequality constraints results in a multi-objective quadratic program based controller that is implemented on a multi-domain hybrid system model of an underactuated bipedal robot. The end result is stable periodic walking on the full-order model that shows remarkable similarity to the SLIP gait from which it was derived.

Ayonga Hereid

Assistant Professor of Mechanical Engineering

My research aims to develop computational and theoretical tools to mitigate the high dimensionality and nonlinearity present in robot control and motion planning problems.