Time dependent control Lyapunov functions and hybrid zero dynamics for stable robotic locomotion
Abstract
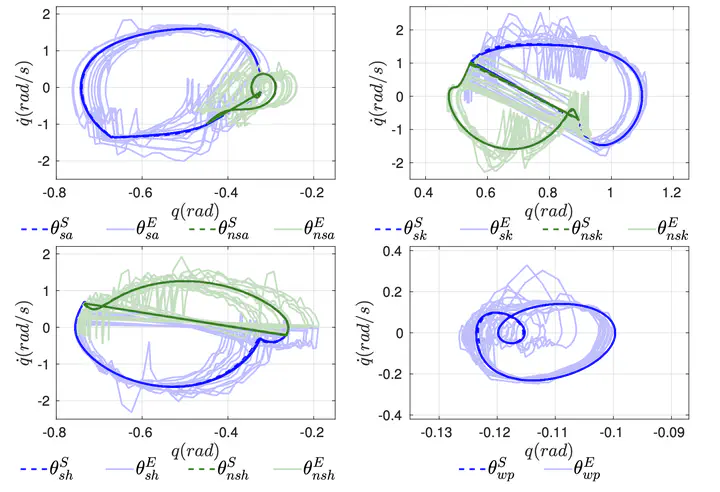
Implementing state-based parameterized periodic trajectories on complex robotic systems, e.g., humanoid robots, can lead to instability due to sensor noise exacerbated by dynamic movements. As a means of understanding this phenomenon, and motivated by field testing on the humanoid robot DURUS, this paper presents sufficient conditions for the boundedness of hybrid periodic orbits (i.e., boundedness of walking gaits) for time dependent control Lyapunov functions. In particular, this paper considers virtual constraints that yield hybrid zero dynamics with desired outputs that are a function of time or a state-based phase variable. If the difference between the phase variable and time is bounded, we establish exponential boundedness to the zero dynamics surface. These results are extended to hybrid dynamical systems, establishing exponential boundedness of hybrid periodic orbits, i.e., we show that stable walking can be achieved through time-based implementations of state-based virtual constraints. These results are verified on the bipedal humanoid robot DURUS both in simulation and experimentally; it is demonstrated that a close match between time based tracking and state based tracking can be achieved as long as there is a close match between the time and phase based desired output trajectories.