Input to state stabilizing control lyapunov functions for robust bipedal robotic locomotion

Abstract

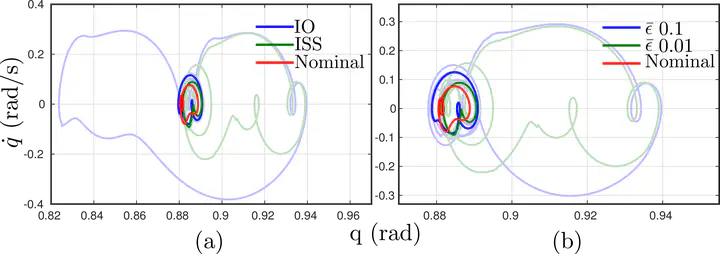
This paper analyzes the input to state stability properties of controllers which stabilize hybrid periodic orbits. Systems that are input to state stable tend to be robust to modeling and sensing uncertainties. The main contribution of this paper is in the construction of control Lyapunov functions that do not just stabilize, but also input to state stabilize a given hybrid system. Bipedal robotic walking, which can be naturally modeled as a hybrid system, is analyzed under this class of controllers. Specifically, we will select a class of controllers via rapidly exponentially stabilizing control Lyapunov functions that stabilize bipedal robotic walking; typically modeled as hybrid periodic orbits. We will show with simulation results that given the control Lyapunov functions and the associated set of stabilizing controllers, there exist input to state stabilizing control Lyapunov functions and the associated set of controllers that input to state stabilize the given periodic orbit.

Ayonga Hereid

Assistant Professor of Mechanical Engineering

My research aims to develop computational and theoretical tools to mitigate the high dimensionality and nonlinearity present in robot control and motion planning problems.