Abstract
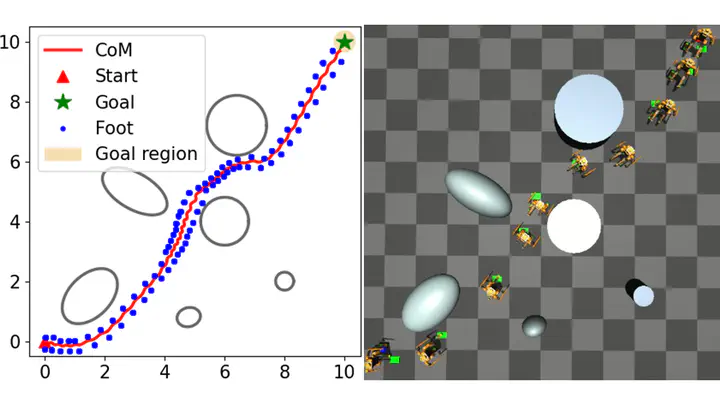
Safe path and gait planning are essential for bipedal robots to navigate complex real-world environments. The prevailing approaches often plan the path and gait separately in a hierarchical fashion, potentially resulting in unsafe movements due to neglecting the physical constraints of walking robots. A safety-critical path must not only avoid obstacles but also ensure that the robot’s gaits are subject to its dynamic and kinematic constraints. This work presents a novel approach that unifies path planning and gait planning via a Model Predictive Control (MPC) using the Linear Inverted Pendulum (LIP) model representing bipedal locomotion. This approach considers environmental constraints, such as obstacles, and the robot’s kinematics and dynamics constraints. By using discrete-time Control Barrier Functions for obstacle avoidance, our approach generates the next foot landing position, ensuring robust walking gaits and a safe navigation path within clustered environments. We validated our proposed approach in simulation using a Digit robot in 20 randomly created environments. The results demonstrate improved performance in terms of safety and robustness when compared to hierarchical path and gait planning frameworks.
Chengyang Peng
Ph.D. Student
My research interests include bipedal robotic walking, motion and path planning, and control barrier functions.
Victor Paredes
Ph.D. Candidate
I am a PhD candidate at The Ohio State University. My research endeavors are centered upon humanoids and exoskeleton devices.
Guillermo A Castillo
Ph.D. Candidate
I am a Ph.D. candidate in Electrical and Computer Engineering at The Ohio State University.
Ayonga Hereid
Assistant Professor of Mechanical Engineering
My research aims to develop computational and theoretical tools to mitigate the high dimensionality and nonlinearity present in robot control and motion planning problems.